Braess paradoksu, bir yol ağına bir veya daha fazla yol eklemenin, genel trafik akışını yavaşlatabileceğini ifade eden bir gözlemdir. Bu paradoks ilk olarak 1920 yılında Arthur Pigou tarafından keşfedilmiş ve daha sonra 1968’de Alman matematikçi Dietrich Braess‘in adıyla anılmıştır.

Bu paradoksun, elektrik şebekeleri ve biyolojik sistemler gibi alanlarda da benzerlikleri olabileceği düşünülmektedir. Teorik olarak, arızalı bir ağın iyileştirilmesinin, belirli kısımlarının kaldırılmasıyla mümkün olabileceği öne sürülmüştür. Paradoks, mevcut ana yolların kapatılması durumunda trafik akışının iyileştiği bazı durumları açıklamak için kullanılmıştır.

Almanya‘daki Ruhr Üniversitesi‘nde matematikçi olan Dietrich Braess, trafik modelleme üzerinde çalışırken bir yol ağına yeni bir yol eklenmesinin trafiğin akışını engelleyebileceğini fark etti. Braess’in fikri, her sürücünün en hızlı güzergahı seçmek için bireysel çıkarına uygun en iyi kararı verdiği durumlarda, bir kestirme yolun aşırı sık tercih edilmesinin tüm sürücüler için en kısa seyahat sürelerini engelleyebileceği yönündeydi. Daha resmi bir ifadeyle, Braess’in keşfinin ardındaki fikir, Nash dengesi ile bir ağdaki en iyi genel akışın aynı şey olmayabileceğidir

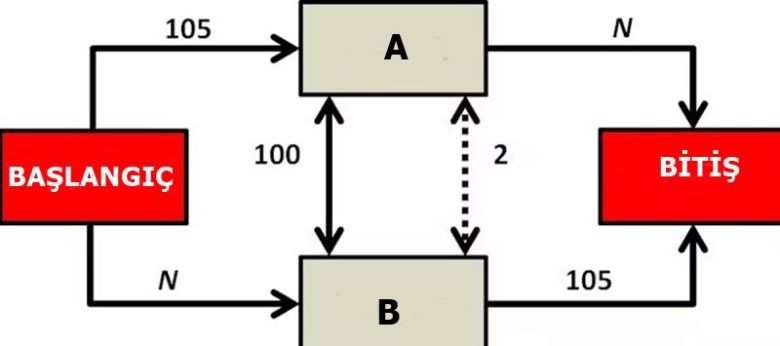
Paradoks şu şekilde ifade edilmektedir:

“Bir yol ağının her noktası için, oradan hareket eden araçların sayısı ve araçların varış noktası verilsin. Bu koşullar altında, trafik akışının dağılımını tahmin etmek istenir. Bir caddenin diğerine tercih edilip edilmeyeceği, yalnızca yolun kalitesine değil, aynı zamanda akış yoğunluğuna da bağlıdır. Her sürücü kendisi için en avantajlı görünen yolu seçerse, ortaya çıkan seyahat süreleri en az olmak zorunda değildir. Dahası, bir örnekle gösterilmektedir ki, yol ağına yapılan bir genişleme, trafiğin yeniden dağılımına neden olarak bireysel seyahat sürelerinin uzamasına yol açabilir.”

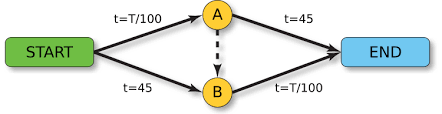
Bir ağa ek kapasite eklemek, hareket eden varlıkların güzergahlarını bencilce seçmesi durumunda, bazı durumlarda genel performansı azaltabilir. Bunun nedeni, böyle bir sistemin Nash dengesinin her zaman optimal olmamasıdır. Ağdaki değişiklik, yeni bir oyun yapısı oluşturur ve bu, çok oyunculu bir tutsak ikilemi senaryosuna yol açar. Nash dengesinde, sürücülerin güzergahlarını değiştirmek için bir teşvikleri yoktur. Sistem Nash dengesinde olmadığında ise bireysel sürücüler, güzergahlarını değiştirerek seyahat sürelerini iyileştirebilir. Braess paradoksu durumunda, sürücüler genel performans düşüşüne rağmen Nash dengesine ulaşana kadar güzergahlarını değiştirmeye devam ederler.

Gecikme fonksiyonları doğrusal olduğunda, bir kenar eklemek, denge noktasında toplam seyahat süresini 4/3’ten daha fazla kötüleştiremez.